벡터사이의 각도
# 첫번째 방법
두 벡터 U와 V가 있을때 의 두 벡터간의 내적은 U●V라고 표시 합니다.
그럼 U●V를 계산하는 공식을 알아 보겠습니다.
[1] U●V = ( (Ux * Vx) + (Uy * Vy) + (Uz * Vz)으로 나옵니다.
그리고 또 다른 공식은
[2] U●V = |U| * |B| * cos(#세타)으로도 나옵니다.
여기서 잠깐 내적의 특징에 대해 알아보겠습니다.
위 [1]번의 공식에 의해 나온 값은 두 벡터간의 각도에 있어서 중요한
정보를 담고 있습니다.
[1]의 공식에 의해 나온 값이 0이면 두벡터간의 각도가 90도 입니다.
[1]의 공식에 의해 나온 값이 0보다 작다면( 0 > U●V ) 두벡터간의 각도는 90도보다 큽니다.
[1]의 공식에 의해 나온 값이 0보다 크다면( 0 < U●V ) 두벡터간의 각도는 90도보다 작습니다.
결과를 표면 내적은 특정한 정보를 찾는데 유용하게 쓰이겠죠??
그럼 우리가 알고 싶은 것은 위의 공식들을 이용해 실재 두벡터간의 각도를 구하는 것 입니다.
위의 공식들을 다시 풀어보면 다음과 같이 나옵니다.
[1]과 [2]의 공식을 조합해 봅시다.
[1] U●V = ( (Ux * Vx) + (Uy * Vy) + (Uz * Vz);
[2] U●V = |U| * |B| * cos(#세타);
우리가 알고 싶은 정보는 cos(#세타)에 들어 있기 때문에 두공식을 이용해 좌우로 이동시켜 보면
U●V
[3] cos(#세타) = ----------- 가 나오고
|U| * |V|
이 공식에서 실재 알고자 하는 라디안 값을 추려내게 되면 다음과 같은 공식이 됩니다.
( ( (Ux * Vx) + (Uy * Vy) + (Uz * Vz) )
(라디안(각도)) #세타 = (아코사인)acos{ --------------------------------- } 이 나옵니다.
( |U| * |V| )
우선 위 공식의 두 대치된 오른쪽에서 큰 괄호 안을 살펴보겠습니다.
(U●V) / (|U| * |V|)에서 우리가 알고자 하는 최종 정보(각도)를 얻는데는 벡터의 크기(길이)
가 몇이든 상관이 없기 때문에 이 두 벡터를 단위 벡터로 만들면 좀더 계산하기 쉬운 공식으로
바뀌게 됩니다.
(|U| * |V|)값이 모두 1길이의 단위 벡터가 되면 위 공식에서 나눗셈 부분이
(U●V) / 1 이 되기 때문에 남는 공식은 다음과 같이 되겠죠.
#세타 = acos( U●V = ( (Ux * Vx) + (Uy * Vy) + (Uz * Vz) );
정말 단순화 되었죠 ^^?
acos(x)함수의 인자로 들어가는 값은 다음과 같습니다.
-1 >= x <= 1
acos(-1) ~ acos(1)이라는 범위는 최종 라디안 값의 0 ~ 파이 값을 가집니다.
acos(-1) = 0; [두벡터의 각이 0도를 의미]
acos(0) = 파이 / 2; [두벡터의 각이 90도를 의미]
acos(1) = 파이; [두벡터의 각이 180도를 의미]
위에서 본 것처럼 acos( U●V )값을 통해 나온 값이 라디안 값으로 표시되는 최종 각도가 됩니다.
***** acos(x)를 계산 하는 공식을 나름데로 만들어 봤습니다 정확히 맞을지는 잘.. ^^; *****
acos(x) = 파이 * ( (1.0 + x) / 2.0 )
x는 -1 부터 1의 범위이고 만약 x가 1이라면
두 벡터의 각도는 [180도 = (radian값)파이가 나요죠 => 3.141592~]
그럼 위의 공식에 대입해 보면 구하고자 했던 각도값(radian)은
acos(1) = 3.141592 * ( (1.0 + 1) / 2.0 ) = 3.141592 가 나옴니다.
#2. 두번째 방법
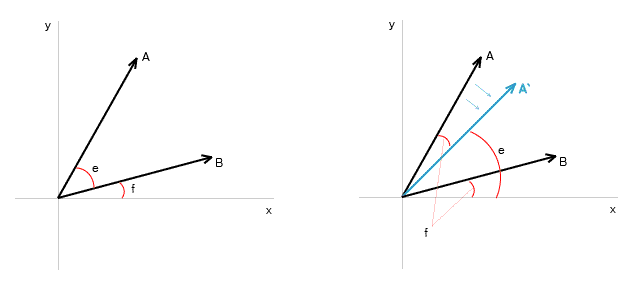
벡터간의 각도는 일반적으로 벡터 내적의 정의로 구합니다만
저는 조금 다른 방향으로 생각해 보았습니다.
그림을 보시죠.
벡터 A, B 사이의 각 e를 구하려고 하는데 벡터 A를 벡터 B와 x축과의 각도 f만큼
회전해서 A`를 구한다면 A`와 x축과의 각도는 e 가 된다는 생각입니다.
그래서 벡터 A의 성분 (x1, y1)에 대해 회전된 벡터 A` (x`, y`)를 구해보면...
x` = cos(f)*x1 - sin(f)*y1
y` = sin(f)*x1 + cos(f)*y1
f각을 구한후 sin, cos를 호출해야 하죠.
그런데 우리는 벡터 B의 성분을 알고있습니다.
벡터 B의 성분 (x2, y2) 와 B의 길이 |B| 를 식에 대입하면...
x` = (x2/|B|)*x1 - (y2/|B|)*y1 = (x2*x1 - y2*y1)/|B|
y` = (y2/|B|)*x1 + (x2/|B|)*y1 = (y2*x1 + x2*y1)/|B|
그런데 이 식 그대로 회전하면 반대로 회전하게 됩니다.
방향을 바꿔줘야 하는데 y2의 부호만 바꿔주면 됩니다.
또하나! 우리가 구하려는건 각도뿐이며 A`의 크기는 상관없으므로 |B|로
나눠준것을 생략할수 있겠죠.. 그래서 최종 공식은...
x` = x2*x1 + y2*y1
y` = x2*y1 - y2*x1
이 벡터와 x 축과의 각도를 구하면 됩니다. ArcTan2를 쓰면되겠죠?
e = ArcTan2 (x2*y1 - y2*x1, x2*x1 + y2*y1)
한줄로 나왔습니다. 간단하지요?
다만 이 방법은 2D 벡터에만 유효합니다.
3D 공식도 세울수는 있지만 코사인 내적 공식과 연산량이 거의 같더군요.
'소프트웨어' 카테고리의 다른 글
| 국내외 3D 네비게이션 동영상 (1) | 2008.03.06 |
|---|---|
| solaris9 port open (2) | 2008.01.29 |
| 자바 zip 압축파일 핸들링 (4) | 2008.01.24 |
 열두마리들의 고양이들과 함께 생활하는 개발자의 일상과 이런저런 이야기들...
열두마리들의 고양이들과 함께 생활하는 개발자의 일상과 이런저런 이야기들...
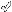 CSS
CSS